Appearance
WTF DeFi 系列 - 何为CPMM?何为CLMM?
传统订单簿模型(Order Book Model) vs 自动做市商模型(AMM)
传统订单簿模型(Order Book Model)
这是中心化交易所(CEX)使用的交易撮合模型,资产交易就像是一个被精心组织的市场。想象一下传统的交易所,在这里:
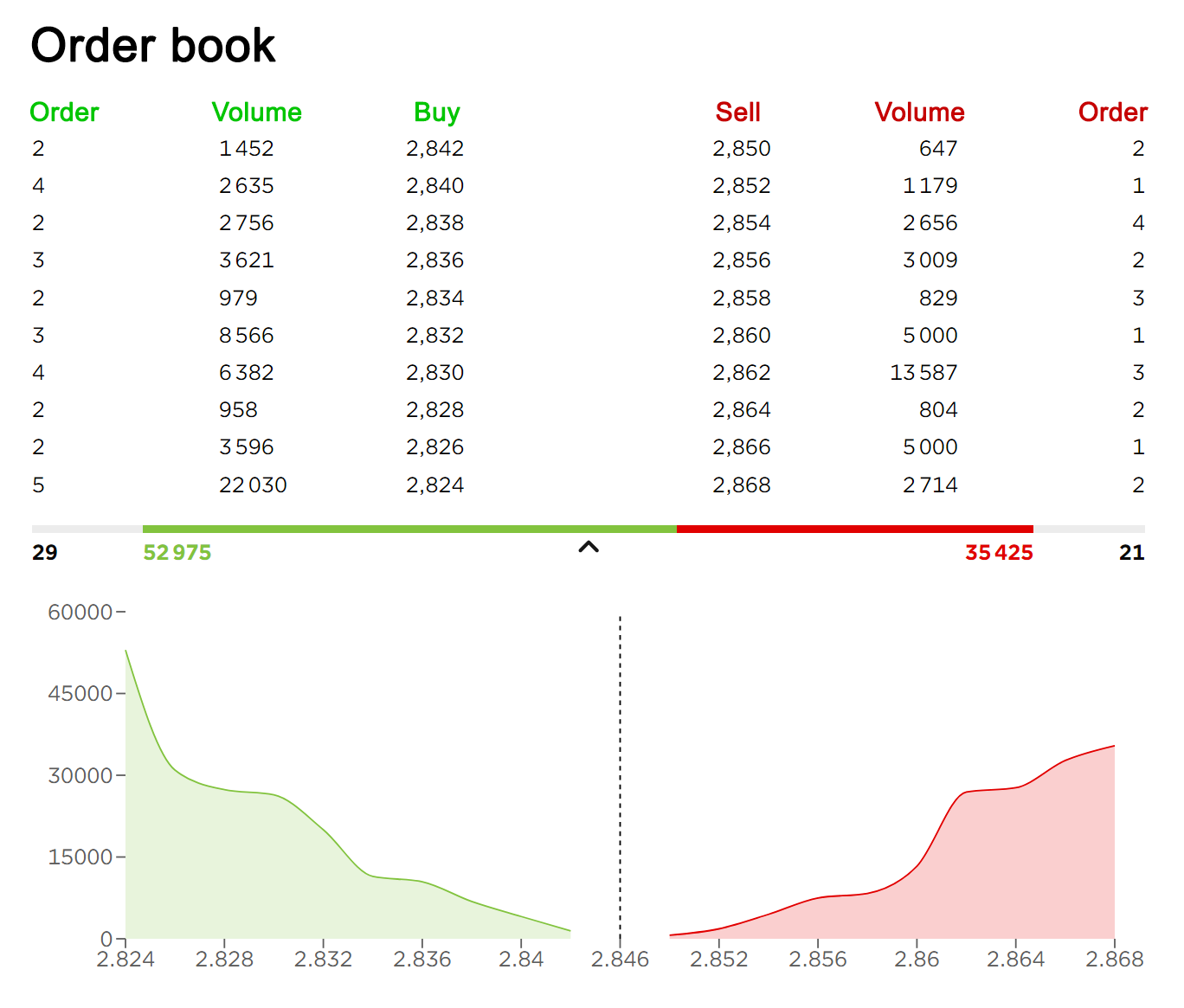
- 所有买卖订单按照价格高低排列在订单簿中;
- 买单(Bids,又名竞价单)按价格从高到低排列,卖单(Asks,又名询价单)按价格从低到高排列;
- 当买卖价格匹配时,交易自动达成;
- 交易深度取决于订单簿中的订单数量和每笔订单的额度;
- 价格由市场供需决定,体现了真实的市场意愿。
自动做市商模型(AMM)
这是去中心化交易所(DEX)常用的创新模型,运作方式完全不同:
- 不需要买卖双方配对,而是使用算法和流动性池;
- 通常采用恒定乘积公式(x * y = k),其中 x 和 y 是池中两种代币的数量,k 是常数;
- 用户直接与流动性池交互,而不是与其他交易者配对;
- 价格由池中资产比例自动计算得出;
- 任何人都可以成为流动性提供者(LP),获得交易费用收入。
两种模型的对比
- AMM 的优势:
- 永续流动性:任何时候都能交易,不用等待对手方
- 去中心化程度更高:无需中心化撮合
- 操作简单:用户只需选择想要交换的代币数量
- 自动定价:不需要人为报价
- AMM的劣势:
- 滑点较大:特别是大额交易时
- 无常损失风险:流动性提供者面临代币价格变化带来的损失
- 资金利用效率较低:需要预先锁定大量资金在池中
- 价格反应较慢:对市场价格变化的反应可能滞后
用一个通俗易懂的例子解释下两者的区别:
假设您想买入1个ETH。在订单簿模型中,您需要查看卖单列表,找到合适的价格(比如1910 USDT)下单,然后等待撮合。而在AMM模型中,您只需要直接与流动性池交互,系统会根据公式自动计算您需要支付的USDT数量。
这就像是在传统市场和自动售货机之间的区别:订单簿模型像是一个供需双方讨价还价的市场,而AMM则更像一个24小时运转的自动售货机,只要投入相应的币就能立即获得想要的商品。
不断迭代的自动做市商模型(AMM)。何为CPMM?何为CLMM?
恒定乘积做市商(Constant Product Market Maker,CPMM)
CPMM 模型是最经典的 AMM 模型,由 Uniswap V2 首创,核心公式:x * y = k(x 和 y 是两种代币的数量,k 是常数),形成一条双曲线形的价格曲线。
- 优点:
- 实现简单,易于理解
- 始终保证有流动性
- 系统非常稳定
- 缺点:
- 资金效率较低,因为流动性分散在全价格范围
- 滑点较大
- 无法针对不同价格区间优化
让我们通过一个具体的交易场景来解释 CPMM 的运行机制:假设 SOL 当前市场价格是 100 USDC,有人想要卖出 50 SOL,此时 CPMM 的表现(比如 Orca v1,Uniswap v2):
- 初始状态:池子中有 1000 SOL 和 100,000 USDC
- 当卖出 50 SOL 时:
- 步骤 1:计算常数 k
k = 1000 * 100,000 = 100,000,000 - 步骤 2:计算交易结果
新的 SOL 数量 = 1000 + 50 = 1050 新的 USDC 数量 = 100,000,000 / 1050 ≈ 95,238.10 USDC 获得量 = 100,000 - 95,238.10 = 4,761.90 - 步骤 3:计算平均成交价格
平均价格 = 4,761.90 / 50 ≈ 95.24 USDC/SOL - 步骤 4:计算滑点
初始价格 = 100 USDC/SOL 滑点 = (100 - 95.24) / 100 * 100% = 4.76%
- 步骤 1:计算常数 k
集中流动性做市商(Concentrated Liquidity Market Maker,CLMM)
CLMM 模型是 Uniswap 团队推出的新版 AMM 模型(Uniswap V2),核心特点是允许流动性提供者选择特定的价格区间提供流动性,旨在解决 V2 版本的缺点 - 资金效率较低。
- 优点:
- 大幅提高资金效率
- 让LP可以模拟限价单
- 在主流交易价格区间提供更好的深度
- 缺点:
- 管理成本更高
- 需要主动管理以避免价格偏离区间
- 对普通用户来说较难理解
CLMM 的关键创新是引入了价格区间和虚拟储备的概念,这与传统的 CPMM 有很大不同。在传统的 CPMM 中,我们有:x * y = k (其中 x 和 y 是实际储备)。但在 CLMM 中,我们使用:(x + virtual_x) * (y + virtual_y) = k,这里的 virtual_x 和 virtual_y 是根据价格区间计算出的虚拟储备量。
当价格在目标区间内时,CLMM 通过以下方式发现更好的成交价格:
- 计算价格影响:
price_impact = initial_price * (1 - ((x_delta) / x))这个计算告诉我们交易会把价格推到什么位置,从而决定使用哪种流动性曲线。
- 计算流动性深度:
# 池子的基础流动性
L = sqrt(k)
# 增强后的流动性,full_range 是完整价格范围,target_range 是目标价格区间
L' = L * (full_range / target_range)为了理解价格区间和流动性集中的思想,想象下一个放大镜,它只关注 95-105 USDC 这个价格区间,在这个区间内,我们把原本分散在更大范围(比如 50-150 USDC)的流动性都集中到这里。
这样做的好处有:
- 把原本分散在较大价格范围的流动性集中到小范围内
- 在目标区间内,交易深度增加了 10 倍
- 流动性提供者的资金使用效率更高
- 可以针对不同交易对设置最适合的价格区间
- 相同的交易量产生更小的价格变动
- 交易者获得更好的价格
- 迭代式的价格发现机制
在 CLMM 中,当我们要进行交易时,实际上是通过一个迭代的过程来找到最终成交价。这个过程类似于解一个方程:
- 初始条件:
- 初始价格 P₁ = 100 USDC/SOL
- 要卖出的数量 ΔX = 50 SOL
- 价格区间 = [95, 105]
- 流动性深度 L(增强后的流动性) = 100,000
- 价格发现过程:
- 设定搜索范围:最低价格 = 95 USDC(价格区间下限),最高价格 = 100 USDC(当前价格)
- 迭代过程:python
# -*- coding: utf-8 -*- import math import numpy as np from typing import Tuple def find_final_price( initial_sol: float, initial_usdc: float, delta_sol: float, L: float, price_range: Tuple[float, float] ) -> float: """ 通过二分查找方法找到最终价格 参数: initial_sol: 初始 SOL 数量 initial_usdc: 初始 USDC 数量 delta_sol: 要交易的 SOL 数量 L: 流动性深度 price_range: (最小价格, 最大价格) """ def calculate_delta_y(p1: float, p2: float) -> float: """计算给定价格区间内的 USDC 变化量""" return L * (np.sqrt(p1) - np.sqrt(p2)) def calculate_delta_x(p1: float, p2: float) -> float: """计算给定价格区间内的 SOL 变化量""" return L * (1/np.sqrt(p2) - 1/np.sqrt(p1)) # 初始价格 p1 = initial_usdc / initial_sol # 设定搜索范围 min_price = price_range[0] max_price = p1 target_delta_x = delta_sol tolerance = 0.01 # 二分查找最终价格 while max_price - min_price > tolerance: mid_price = (min_price + max_price) / 2 print(mid_price) current_delta_x = calculate_delta_x(p1, mid_price) if abs(current_delta_x - target_delta_x) < tolerance: return mid_price elif current_delta_x < target_delta_x: max_price = mid_price else: min_price = mid_price return (min_price + max_price) / 2 if __name__ == '__main__': # 示例参数 initial_sol = 1000 initial_usdc = 100000 delta_sol = 50 price_range = (95, 105) # 增强后的流动性 L = math.sqrt(initial_sol * initial_usdc) * ((150 - 50) / (105 - 95)) # 找到最终价格 final_price = find_final_price( initial_sol, initial_usdc, delta_sol, L, price_range )- 第1次尝试:价格 = 97.5 USDC,计算得到的 SOL ≈ 127.39 SOL(太多)
- 第2次尝试:价格 = 98.75 USDC,计算得到的 SOL ≈ 63.09 SOL(太多)
- 第3次尝试:价格 = 99.375 USDC,计算得到的 SOL ≈ 31.40 SOL(太少)
- 第4次尝试:价格 = 99.0625 USDC,计算得到的 SOL ≈ 47.21 SOL(少了)
- 第5次尝试:价格 = 98.90625 USDC,计算得到的 SOL ≈ 55.14 SOL(多了)
- 第6次尝试:价格 = 98.984375 USDC,计算得到的 SOL ≈ 51.17 SOL(多了一点)
- 第7次尝试:价格 = 99.0234375 USDC,计算得到的 SOL ≈ 49.19 SOL(少了一点)
- 第8次尝试:价格 = 99.00390625 USDC,计算得到的 SOL ≈ 50.18 SOL(多了一点点)
- 第9次尝试:价格 = 99.013671875 USDC,计算得到的 SOL ≈ 49.68 SOL(差不多可以了)
- 继续迭代直到找到更合适的价格...
参考 CPMM 的实际交易例子,让我们用同一个交易场景来解释 CLMM 的运行机制:假设 SOL 当前市场价格是 100 USDC,有人想要卖出 50 SOL,此时 CLMM 的表现(比如 Orca v2,Uniswap v3,Raydium):
- 同样的初始状态:池子中有 1000 SOL 和 100,000 USDC,但流动性集中在 95-105 USDC 价格区间
- 卖出 50 SOL 时:
- 步骤 1:检查价格影响
预期价格 = 100 * (1 - 50/1000) = 95 USDC/SOL 95 在 90-110 价格区间内 - 步骤 2:计算流动性集中效应
完整范围 = 100 * (1.5 - 0.5)= 100(假设是当前价格的 0.5-1.5 倍) 目标范围 = 105 - 95 = 10 集中倍数(浓度系数) = 100/10 = 10 基础流动性 L = √(x * y) = √(1000 * 100,000) = 10,000 增强后的流动性 L' = 10,000 * 10 = 100,000 - 步骤 3:价格范围内的实际交易计算 - 当在价格范围内进行交易时,需要使用积分公式计算实际获得的 USDC
∆y = L * (√P₁ - √P₂),其中: L = 增强后的流动性 = 100,000 P₁ = 初始价格 = 100 P₂ = 交易后价格 ≈ 99.014获得的 USDC = 100,000 * (1/√100 - 1/√99.014) ≈ 4945.23 平均成交价格 = 4945.22 / 50 = 98.9 USDC/SOL - 步骤 4:实际滑点约为 1.1%
- 步骤 1:检查价格影响
值得注意的是如果价格超出设定区间,会自动切换到更稀疏的流动性曲线。